Diameter
| Geometry |
|---|
 |
| Geometers |
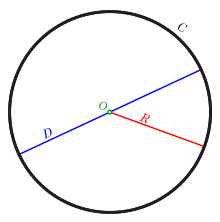
In geometry, a diameter of a circle is any straight line segment that passes through the centre of the circle and whose endpoints lie on the circle. It can also be defined as the longest chord of the circle. Both definitions are also valid for the diameter of a sphere.
In more modern usage, the length of a diameter is also called the diameter. In this sense one speaks of the diameter rather than a diameter (which refers to the line segment itself), because all diameters of a circle or sphere have the same length, this being twice the radius
The word "diameter" is derived from Ancient Greek: διάμετρος (diametros), "diameter of a circle", from διά (dia), "across, through" and μέτρον (metron), "measure".[1] It is often abbreviated or
Constructions
[edit]With straightedge and compass, a diameter of a given circle can be constructed as the perpendicular bisector of an arbitrary chord. Drawing two diameters in this way can be used to locate the center of a circle, as their crossing point.[2] To construct a diameter parallel to a given line, choose the chord to be perpendicular to the line.
The circle having a given line segment as its diameter can be constructed by straightedge and compass, by finding the midpoint of the segment and then drawing the circle centered at the midpoint through one of the ends of the line segment.
Symbol
[edit]

The symbol or variable for diameter, ⌀, is sometimes used in technical drawings or specifications as a prefix or suffix for a number (e.g. "⌀ 55 mm"), indicating that it represents diameter.[3] Photographic filter thread sizes are often denoted in this way.[4]
The symbol has a code point in Unicode at U+2300 ⌀ DIAMETER SIGN, in the Miscellaneous Technical set. It should not be confused with several other characters (such as U+00D8 Ø LATIN CAPITAL LETTER O WITH STROKE or U+2205 ∅ EMPTY SET) that resemble it but have unrelated meanings.[5] It has the compose sequence Composedi.[6]
Generalizations
[edit]The definitions given above are only valid for circles and spheres. However, they are special cases of a more general definition that is valid for any kind of -dimensional object, or a set of scattered points. The diameter of a set is the least upper bound of the set of all distances between pairs of points in the subset.
A different and incompatible definition is sometimes used for the diameter of a conic section. In this context, a diameter is any chord which passes through the conic's centre. A diameter of an ellipse is any line passing through the centre of the ellipse.[7] Half of any such diameter may be called a semidiameter, although this term is most often a synonym for the radius of a circle or sphere.[8] The longest diameter is called the major axis. Conjugate diameters are a pair of diameters where one is parallel to a tangent to the ellipse at the endpoint of the other diameter.
Several kinds of object can be measured by equivalent diameter, the diameter of a circular or spherical approximation to the object. This includes hydraulic diameter, the equivalent diameter of a channel or pipe through which liquid flows, and the Sauter mean diameter of a collection of particles.
The diameter of a circle is exactly twice its radius. However, this is true only for a circle, and only in the Euclidean metric. Jung's theorem provides more general inequalities relating the diameter to the radius.
See also
[edit]- Caliper, micrometer, tools for measuring diameters
- Eratosthenes, who calculated the diameter of the Earth around 240 BC.
- Tangent lines to circles – Line which touches a circle at exactly one point
References
[edit]- ^ "Diameter—Origin and meaning of diameter by Online Etymology Dictionary". www.etymonline.com.
- ^ "6-66 Finding the center of a circle". General Drafting. Technical manual, TM 5-581A, United States Department of the Army. U.S. Government Printing Office. 1972. p. 6-32.
- ^ Puncochar, Daniel E. (1997). Interpretation of Geometric Dimensioning and Tolerancing. Industrial Press Inc. p. 5. ISBN 9780831130725.
- ^ Ciaglia, Joseph (2002). Introduction to Digital Photography. Prentice Hall. p. 9. ISBN 9780130321367.
The filter diameter (in mm) usually follows the symbol ⌀
- ^ Korpela, Jukka K. (2006). Unicode Explained. O'Reilly Media, Inc. p. 171. ISBN 9780596101213.
- ^ Monniaux, David. "UTF-8 (Unicode) compose sequence". Retrieved 2018-07-13.
- ^ Bogomolny, Alexander. "Conjugate Diameters in Ellipse". www.cut-the-knot.org.
- ^ Raphson, Joseph; Ozanam, Jacques (1702). A Mathematical Dictionary. J. Nicholson, and T. Leigh and D. Midwinter. p. 26.






